华罗庚

在英明领袖华主席发出 “提高整个中华民族科学文化水平” 的伟大号召下，我国科技教育战线出现了崭新的局面．经国务院批准，教育部和全国科协联合举办的全国八省、市中学数学竞赛已经告一段落．在这期间，各地老师们为了培养下一代，为了向四个现代化进军，十分辛劳地出了不少试题．各方面要求把这些试题汇总出版．

这样的事，只有在华主席为首的党中央一举粉碎 “四人帮” 后，在抓纲治国、拨乱反正初见成效后才会出现，其影响遍及全国，其意义之深远是难以估计的．我参与其事的体会是说不尽的，在这儿只谈些我和同学们一同参加考试后的一些体会，和我所知道的部分试题背景．很可能挂一湍万，不能道出出题老师们的全部心意．但抛砖引玉总比藏而不露易于受教益，因此把一些认识写在下面，敬待指教．

1. 从量地看阶级剥削

全国试题第二试第 4 题，是一个量地问题． 一块四边形的土地要丈量它的面积，解放前，北方地主是用两组对边中点连线长度的乘积作为面积，而南方地主是用两组对边边长平均值的乘积作为面积．实际上，四边形真正的面积 $\leqslant$ 两组对边中点连线长度的乘积 $\leqslant$ 两组对边边长平均值的乘积．这也就是说，北方地主和南方地主的量法都是把土地量大了．面积量大了农民就得多交租，地主得到好处．农民由于缺乏文化，对这种剥削比对大斗小秤更难于发觉，我们证明这个题目的方法是这样的，把四边形沿对边中点连线划成四块搬到图 2 的位置，得到一个平行四边形．它的两边就是原四边形对边中点连线 (这里利用了对边中点连线相互平分的性质，请同学们想一想，这点能如何简单地证明一个平行四边形的面积总是≤两边长乘积，因而我们证明了第一个不等式．在原四边形的右边排上同样的四块得到图 3．利用三角形两边之和大于第三边，就得到对边边长平均值大于另一组对边中点连线，这样就证明了第二个不等式．

图 1	图 2	图 3

2. 物理模型与数学方法

北京试题第二试第 1 题，其实际背景是从光行最速原理推出入射角等于反射角，在数学上涉及了对称原理，这是一道好题目．

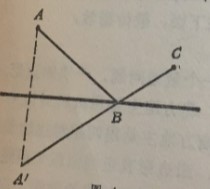图 4

光线从 $A$ 经 $B$ 到 $C$, $A'$; 是 $A$ 的对称点，利用三角形两边和大于第三边，可见，只有入射角等于反射角时，$AB+BC$ 取最小值．

这次出全国试题时，本来想出从光行最速原理推出关于折射角的问题．虽然用微积的方法，这是很容易的．但由于我们没有想到适合于当前中学生的解法，所以没打采用．

3. 射影几何的基本定理

全国试题第二试第 1 题，包含（仿射几何的拈本原理．苏步行教授在来伯中也建议出问样性成但另－， 形式的脏目 3 已知与一直线 $l$ 平行的一条线段 $AO$, 今要求只用直尺不用圆规平分线段 $AC$, 图 5 就把作图方法告诉了我们，

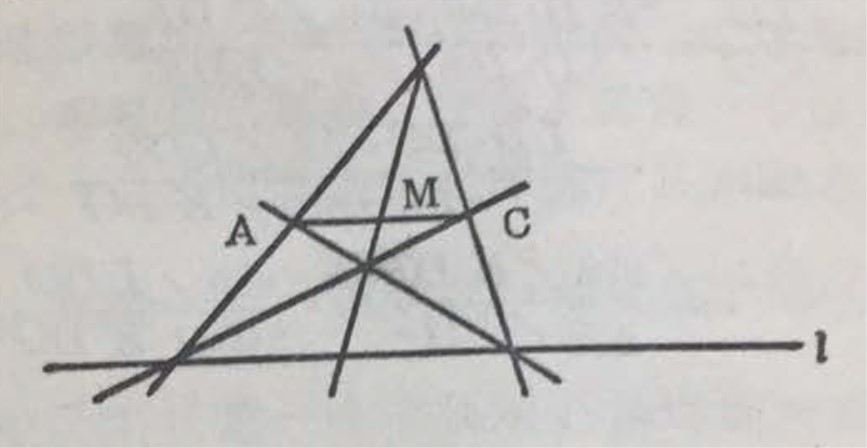图 5

$M$ 点即平分 $AC$．射影几何是仿射几何进一步的发展．在图 5 中去掉 AC 平行于 l 这一条件，就得到另一图形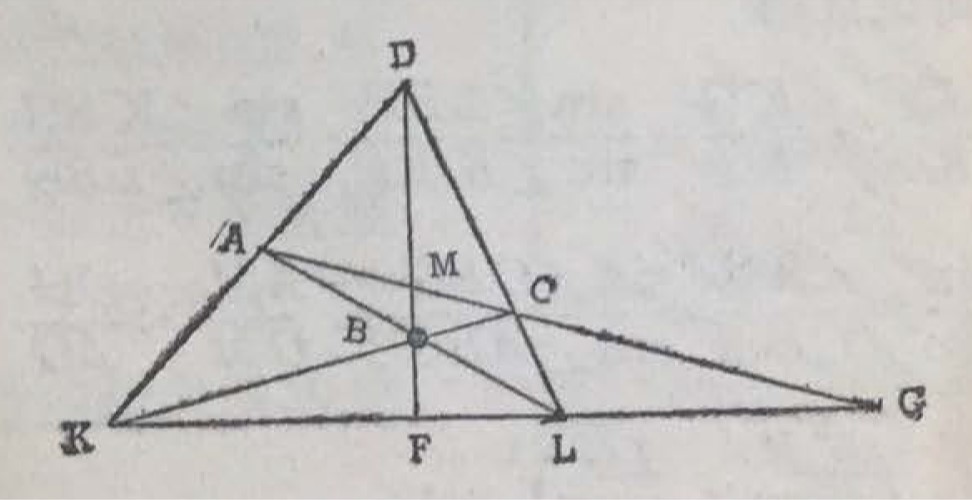（图 6)．

图 6

在图 6 中求证$$\frac { K F } { L F } = \frac { K G } { L G }$$．这里就包含了射影几何的基本原理．将 G 点趋于无穷，图 6 就变为图 5．

我们来证明这个题目. 设 $\triangle K F D$ 中 $KF$ 边上的高为 $h$. 利用 $2\triangle K F D$ 面积 $= K F \cdot h = K D \cdot D F \cdot \sin \angle K D F$, 得到 $$K F = \frac {1} { h } \cdot K D \cdot D F \cdot \sin \angle K D F$$ 同理，再求出 $LF$、$LG$ 与 $KG$ 的类似的表达式．

因而

$$\begin{aligned} \frac { K F } { L F } \cdot \frac { L G } { K G } = \frac { K D \cdot D F \cdot \sin \angle K D F } { L D \cdot D F \cdot \sin \angle L D F } \\ \cdot \frac { L D \cdot D G \cdot \sin \angle L D F } { K D \cdot D G \cdot \sin \angle K D G } \\ = \frac { \sin \angle K D F } { \sin \angle L D F } \cdot \frac { \sin \angle L D G } { \sin \angle K D G } \end{aligned},$$ 同样可得到

$$\frac {A M} { C M } \cdot \frac { C G } { A G } = \frac { \sin \angle A D M } { \sin \angle C D M } \cdot \frac { \sin \angle C D G } { \sin \angle A D G },$$

所以 $$\frac {K F} { L F } \cdot \frac { L G } { K G } = \frac { A M } { C M } \cdot \frac { C G } { A G }.$$ 类似地可以证明 $$\begin{aligned}{ \frac { L F } { K F } \cdot \frac { K G } { L G } = \frac { \sin \angle L B F } { \sin \angle K B F } \cdot \frac { \sin \angle K B G } { \sin \angle L B G } } \\ { = \frac { \sin \angle A B M } { \sin \angle C B M } \cdot \frac { \sin \angle C B G } { \sin \angle A B G } = \frac { A M } { C M } \cdot \frac { C G } { A G } } \end{aligned}$$ 由此可见 $$\left( \frac { K F } { L F } \cdot \frac { L G } { K G } \right) ^ { 2 } = 1.$$ 即证得结论．图 6 也告诉我们，在已知 $K$、$F$、$L$ 三点时，可以只用尺不用圆规作图找到第四点 $G$，使 $F$“内分”$KL$ 的比例于 $G$“外分”$KL$ 的比例．

4. 凸体分割问题

安徽试题第二试第 3 题是说，通过三角形重心的任意一条直线把三角形切成的两块．其面识之比总是在 $\frac {4} { 5 }$ 与 $\frac { 5 } { 4 }$ 之间．这里我们可以想到这样一个问题，在三形内应该选择怎样的点，使得过这点沿任意直线把三角形所切得的两块，其面积之比的变化范最小. 同学们可以证明，这点是选选在三角形的重最好．不只是三角形，平面上任意一个凸的图行，过它的重心沿任一直线把图形切成两块，其面积之比也总是 $\frac { 4 } { 5 }$ 与 $\frac { 5 } { 4 }$ 之间．更进一步，我们也知道三维空间任意一个凸体，过它的重心沿任意一个平面把凸体切成两块，其体积之比总在 $\frac { 27 } { 37 }$ 与 $\frac { 37 } { 27 }$ 之间．要证明这些结论，可能就出乎中学数学的范围了．要证明这些结论，可能就出乎中学数学的范围了．

5. 规划论的一个基本原则

全国试题第二试第 3 题, 可以一般地化为下列的问题: 当点 $(x , y)$ 在平面上一个区域 $\Gamma$(包括边界) 上变动时，求一次函数 $a x + b y$ 的最大值和最小值．

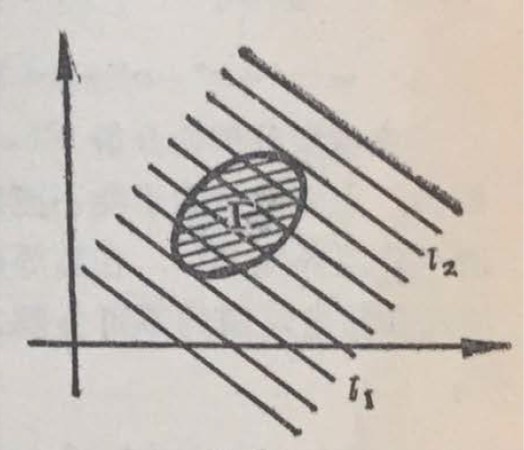图 7

$a x + b y = p$, 当 $p$ 变动时就得到一组互相平行的直线族，与 $\Gamma$ 有公共点的最边缘的两条直线 $l_1$ 和 $l_2$, 就决定了 $a x + b y$ 在 $\Gamma$ 上的最小值和最大值. 可见一次函数的极值总是在 r 的边界上达到．当区域 $\Gamma$ 是一个三角形时，就一定在顶点上达到极值．如果 $\Gamma$ 有一条边与直线族 $a x + b y = p$ 平行，则在条边上 $a x + b y$ 的值都相等，且是最大值或最小值．

6. 分圆多项式不可分解问题

全国试题第二试第 2(1) 题，分解多项式 $$F (x) = x ^ { 12 } + x ^ { 3 } + x ^ { 6 } + x ^ { 3 } + 1$$

在复数范围内可分解为 $$F (x) = \prod _ { k = 1 \atop k = 5,10 } ^ { 14 } \left( x - e ^ { \frac { 2 \pi i } { 15 } k } \right),$$ 在实数范围内可分解为 $$F (x) = \prod _ { k = 1 \atop k = 5 } ^ { 7 } \left( x ^ { 2 } - 2 \cos \frac { 2 k \pi } { 15 } x + 1 \right),$$ 在整数范围内可分解为 $$\begin{aligned} F ( x ) & = \frac { x ^ { 15 } - 1 } { x ^ { 3 } - 1 } = \frac { \left( x ^ { 5 } - 1 \right) \left( x ^ { 10 } + x ^ { 5 } + 1 \right) } { x ^ { 3 } - 1 } \\ & = \left( x ^ { 4 } + x ^ { 3 } + x ^ { 2 } + x + 1 \right) \left( x ^ { 8 } - x ^ { 7 } + x ^ { 4 } + x ^ { 4 } + x ^ { 3 } - x + 1 \right) \end{aligned}.$$

在整数范围内分解 $F(x)$, 这是出题人的原意．在整数范围内，上面两个因子能不能继续分解？这两个多项式都是所谓 “分圆多项式”，在高等数学中可以一般地证明，分圆多项式在整数范围内不可分解．我们现在用初等的方法来证明: $$f _ {1} ( x ) = x ^ { 4 } + x ^ { 3 } + x ^ { 2 } + x + 1.$$ 和 $$f _ {2} ( x ) = x ^ { 8 } - x ^ { 7 } + x ^ { 5 } - x ^ { 4 } + x ^ { 3 } - x + 1,$$ 在整数范围内不可分解．

$f_1(x)$ 和 $f_2(x)$ 都是 $x ^ { 15 } - 1$ 的因子，$x ^ { 15 } - 1$ 除了 1 之外没其他实根，而 1 不是 $f_1(x)$ 和 $f_2(x)$ 的根，所以 $f_1(x)$ 和 $f_2(x)$ 没有实数根．于是它们不可能有奇数次因子．如果 $f_1(x)$ 和 $f_2(x)$ 有二次因子，一定形如 $x ^ { 2 } - 2 \cos \frac { 2 k \pi } { 15 } x + 1$ $( 1 \leqslant k \leqslant 7 \quad k \neq 5 )$，而这时 $\cos \frac { 2 k \pi } { 15 } \neq 0 , \pm \frac { 1 } { 2 } , \pm 1$，所以 $2 \cos \frac { 2 k \pi } { 15 }$ 不是整数，因此 $f_1(x)$ 和 $f_2(x)$ 不可能有二次因子，这样我们就证明了 $f_1(x)$ 不可分解．而 $f_2(x)$ 如果能分解, 只能是 $$f _ {2} ( x ) = \left( x ^ { 4 } + a x ^ { 3 } + b x ^ { 2 } + a x + 1 \right) \left( x ^ { 4 } + c x ^ { 3 } + d x ^ { 2 } + c x + 1 \right),$$

(两个二次式 $x ^ { 2} - 2 \cos \frac { 2 k \pi } { 15 } x + 1$ 相乘得到的四次因子一定是上述形式). 比较等式两边的系数，可得 $$\begin{array} { l } { a + c = - 1 }, \\ { d + a c + b = 0 }, \\ { c + a d + b c + a = 1 }, \\ { 2 + 2 a c + b d = - 1 }. \end{array}$$

第 2 式乘 2 减去第 4 式得 $$(d - 2) ( b - 2 ) = 1,$$ 因而 $$b = d = 2 \pm 1.$$ 由第 3 式得出 $$b = - 2$$ 矛盾，所以 $f_2(x)$ 不可分解．

7. 证明素数定理的一个工具

全国试题第二试第 2(2) 题，来自下列一般问题: 求整数 $a _ { 0 } , a _ { 1 } , \cdots a _ { n }$ 使三角多项式 $$a _ {0} + a _ { 1 } \cos \phi + \dots \cdots + a _ { n } \cos n \phi \geqslant 0 \quad \text{（对一切 $\phi$）}$$ 且适合 $0 <a _ { 0} < a _ { 1 } a _ { 2 } \geqslant 0 , \quad \cdots a _ { n } \geqslant 0,$

并使

$$a = \frac {a _ { 1} + a _ { 2 } + \dots \cdots + a _ { n } } { 2 \left( \sqrt { a _ { 1 } } - \sqrt { a _ { 0 } } \right) ^ { 2 } }$$

最小， 并求这个最小值.

这个问题太难，现在给出下列诸例.

例 1  $n=2$

$$\begin{aligned} 3 + 4 \cos \phi + \cos 2 \phi & = 3 + 4 \cos \phi + 2 \cos ^ { 2 } \phi - 1 \\ & = 2 ( 1 + \cos \phi ) ^ { 2 } \geqslant 0 \end{aligned},$$ $$a = \frac {4 + 1} { 2 ( 2 - \sqrt { 3 } ) ^ { 2 } } = \frac { 35 } { 2 } + 10 \sqrt { 3 } = 34.82.$$

例 2  $n=3$

$$\begin{array} { l } { 5 + 8 \cos \phi + 4 \cos 2 \phi + \cos 3 \phi } \\ { \quad = 5 + 8 \cos \phi + 4 \left( 2 \cos ^ { 2 } \phi - 1 \right) + 4 \cos ^ { 3 } \phi - 3 \cos \phi } \\ { = 4 \cos ^ { 3 } \phi + 8 \cos ^ { 2 } \phi + 5 \cos \phi + 1 } \\ { = ( \cos \phi + 1 ) ( 2 \cos \phi + 1 ) ^ { 2 } \geqslant 0 } \end{array},$$ $$a = \frac {8 + 4 + 1} { 2 ( \sqrt { 8 } - \sqrt { 5 } ) ^ { 2 } } = \frac { 169 } { 18 } + \frac { 26 } { 9 } \sqrt { 10 } = 18.52.$$

例 3  $n=4$

$$\begin{aligned} & 18 + 30 \cos \phi + 17 \cos 2 \phi + 6 \cos 3 \phi + \cos 4 \phi \\ = & 18 + 30 \cos \phi + 17 \left( 2 \cos ^ { 2 } \phi - 1 \right) + 6 \left( 4 \cos ^ { 3 } \phi - 3 \cos \phi \right) \\ & + \left( 8 \cos ^ { 4 } \phi - 8 \cos ^ { 2 } \phi + 1 \right) \\ = & 8 \cos ^ { 4 } \phi + 24 \cos ^ { 3 } \phi + 26 \cos ^ { 2 } \phi + 12 \cos ^ { 3 } \phi + 8 \cos ^ { 2 } \phi \\ = & 2 \left[ \left( 4 \cos ^ { 4 } \phi + 4 \cos ^ { 3 } \phi + \cos ^ { 2 } \phi \right) + \left( 8 \cos ^ { 3 } \phi + 8 \cos ^ { 2 } \phi \right. \right. \\=&2 ( \cos \phi ) + \left( 4 \cos ^ { 2 } \phi + 4 \cos \phi + 1 \right) ] \\ = & 2 ( \cos \phi + 1 ) ^ { 2 } ( 2 \cos \phi + 1 ) ^ { 2 } \geqslant 0 \end{aligned},$$ $$a = \frac {30 + 17 + 6 + 1} { 2 ( \sqrt { 30 } - \sqrt { 18 } ) ^ { 2 } } = 9 + \frac { 27 } { 12 } \sqrt { 15 } = 17.71.$$

例 1、例 2 被用于素数定理的证明，例 3 被用于某些素数函数的上界估计中．

8. 排序问题

全国试题第二试第 5 题，排队提水的问题，在其他一些场合也是会遇到的．例如，有台机床要加工 n 个工件，每个工件需要的加工时间不一样，问应该按照什么次序加工，使总的等待时间最短．同样，如果有两台同样的机床加工 n 个工件，应该怎样安排加工顺序呢? 在这个题目的解法中利用了一条简单而重要的引理．

引理 (a) 表示非负数 $a _ { 1 } , a _ { 2 } , \cdots a _ { n }$，

(b) 表示非负数 $b _ { 1 } , \quad b _ { 2 } , \dots \dots b _ { n }$，

问题 (a)与 (b) 一对一对相乘后相加，何时最大，何时最小?

答案: 同序时最大，倒序时最小．

将 (a) 由小到大排为 $\overline { a } _ { 1 } \leqslant \overline { a } _ { 2 } \leqslant \cdots \leqslant \overline { a }$，
将 ( b ) 由小到大排为 $\overline { b } _ { 1 } \leqslant \overline { b } _ { 2 } \leqslant \cdots \cdots \leqslant \overline { b } _ { n }$,

也就是说

$$\overline {a} _ { 1 } \overline { b } _ { 1 } + \overline { a } _ { 2 } \overline { b } _ { 2 } + \dots \dots + \overline { a } _ { n } \overline { b } _ { n }\quad \text{最大,}$$ $$\overline {a} _ { 1 } \overline { b } _ { n } + \overline { a } _ { 2 } \overline { b } _ { n - 1 } + \dots \dots + \overline { a } _ { n } \overline { b } _ { 1 }\quad\text{最小.}$$

证明 若 $a _ {i} < a _ { j } , b _ { i } < b _ { j }$ 则 $$a _ {i} b _ { i } + a _ { j } b _ { j } - \left( a _ { i } b _ { j } + a _ { j } b _ { i } \right) = \left( a _ { i } - a _ { j } \right) \left( b _ { i } - b _ { j } \right) > 0.$$

可见，在 $i$ 和 $j$ 两个位置上，将同序改为倒序时，和值将减少，由此即可证得引理．

(I) 一个水龙头的情况．若按某一顺序放水时间依次为 $a _ { 1 } , a _ { 2 } , \dots a _ { n }$，则总的等待时间为:

$$\begin{array} { c } { a _ { 1 } + ( a _ { 1 } + a _ { 2 } ) + ( a _ { 1 } + a _ { 2 } + a _ { 3 } ) + \dots + ( a _ { 1 } + a _ { 2 } + \dots +a_n } \\ { \quad = n a _ { 1 } + ( n - 1 ) a _ { 2 } + \dots + 2 a _ { n - 1 } + a _ { n } } \end{array}$$ 在引理中取 $(b) = n , n - 1 , \dots \cdots \cdot 2,1$，可见依 $a_i$ 由小到大的次序放水等待时间最少．

(II) 二个水龙头的情况．首先考虑两个水龙头上人务相等的情况．若一个龙头上按某一顺序放水时间依次为 $ a _ { 1 } + a _ { 2 } + \dots +a_n$ 另一个龙头上按某顺序放水时间依饮为 $a _ { 1 } ^ { \prime } , a _ { 2 } ^ { \prime } , \dots a _ { n } ^ { \prime }$ 则总的等待时间为: $$\begin{array} { c } { n a _ { 1 } + ( n - 1 ) a _ { 2 } + \dots \cdots + a _ { n } + n a _ { 1 } ^ { \prime } + ( n - 1 ) a _ { 2 } ^ { \prime } + \cdots \cdots + a _ { n } ^ { \prime } } \\ { \quad = n a _ { 1 } + n a _ { 1 } ^ { \prime } + ( n - 1 ) a _ { 2 } + ( n - 1 ) a _ { 2 } ^ { \prime } + \cdots \cdots + a _ { n } + a _ { n } ^ { \prime } } \end{array}$$

在引理中取 $(b)$ 为 $n , n , n - 1 , n - 1 , \cdots \cdots 1,1$，可见当 $$a _ {1} \leqslant a _ { 1 } ^ { \prime } \leqslant a _ { 2 } \leqslant a _ { 2 } ^ { \prime } \leqslant \cdots \leqslant a _ { n } \leqslant a _ { n } ^ { \prime }$$ 时，总的花费时间最少．当然使花费时间最少的排法可以不止一个．

若两个龙头上人数不等，则在人数少的龙头上添上一定个数放水时间为零的人，使人数相等，再利用上述引理．

(III) 类似地可以讨论 $n$ 个人 $r$ 个龙头的情况．等待时间最少的排列，就是按照放水时间由小到大的次序，依次在 $r$ 个龙头上放水，哪个龙头上的人打完了水，后面等待着的第一人就上去打水．