什么是双有理几何——2018年菲尔兹奖得主 Caucher Birkar及其工作介绍
Marianne Freiberger/文
张浩/译

鉴于Caucher Birkar1在代数几何这一数学领域中做出的贡献,他被授予2018年菲尔兹奖。这一领域恰如其名:它试图通过代数方程来理解所描述的几何对象。
你在上学时可能会熟悉这种观点:方程$y=2x+1$刻画了一条斜率为2的直线,它与笛卡尔直角坐标系的纵轴相交于$(0,1)$点;类似地,方程$x^2+y^2=1$描述了笛卡尔直角坐标系中以原点为圆心、半径为1的圆(如图 1 ,这可从勾股定理推出)。
这里的圆和直线都是欧几里得平面中代数曲线的例子。这些曲线都是通过代数方程定义的。
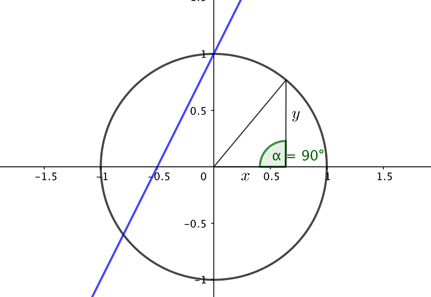 图 1 蓝色直线的方程是 $y=2x+1$,圆的方程是 $x^2+y^2=1$.
图 1 蓝色直线的方程是 $y=2x+1$,圆的方程是 $x^2+y^2=1$.
增加一个维度之后,我们可以考虑代数曲面。三维欧几里得空间中,球心在原点、半径为1的球面就是一个例子。与低一维的圆相比,它由以下代数方程给出
\[ x^2+y^2+z^2=1. \]
正如你可能已经想到的,三维空间中的平面是代数曲面的另一个例子。
但是我们不应止步不前,更多复杂的多项式方程可以定义在其他类型的数(如复数2)上,这会得出代数簇3的一般概念。代数曲线和代数曲面都是代数簇的例子,但一般的代数簇可以更为复杂:它们可以存在于不能被直接看到的高维空间中。但这并没有阻止数学家前进,即便他们遇到很难想象的高维空间,他们仍然发展了研究几何的方式。
给定了已有的无穷多个代数簇之后,一个好点子是把它们按家族分类,就好像分类蝴蝶收藏册一样。回到上面的例子,你也可能会想要按照它们的形状类型来分类:像平面的归为一类,像球面的归为另一类,等等。
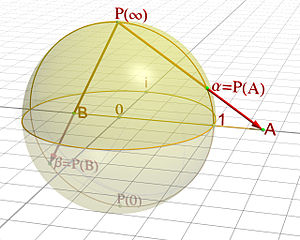 图 2 球极投影将球面上每一点(除去北极点)与赤道平面上的某一点关联起来:对球面上的每一个点p(除去北极点)画出它与北极点之间的连线,这条直线将会与赤道平面交于一点q。图片来源:Jean-Christophe Benoist4
图 2 球极投影将球面上每一点(除去北极点)与赤道平面上的某一点关联起来:对球面上的每一个点p(除去北极点)画出它与北极点之间的连线,这条直线将会与赤道平面交于一点q。图片来源:Jean-Christophe Benoist4
但是你也可以允许更多的灵活性。上图中的投影展示了一个球面去掉一个点可以变换成一个平面:对球面上除去北极点的每一点p,画出它与北极点之间的连线,这条直线将会与赤道平面交于一点q。这样可以把球面上除去北极点的每一点p挪到平面上相应的q点,因此我们的投影将去掉一个点的球面变换成一个平面。从而看起来形状悬殊的平面和球面就建立了联系,当我们给代数曲面分类时要谨记这一点。
我们刚刚考虑的投影是双有理映射5的一个例子。双有理映射可以在更广泛的情形下定义,它可以将更多复杂的代数簇联系起来,而不仅仅是球面和平面。并且有很好的理由说明我们为什么要通过这样的方式将它们联系起来。其中之一是并非所有的代数簇都像上述的平面和球面一样既漂亮又光滑。有一些代数簇含有奇点,粗略地讲是尖点。至少当你在处理某种情形(学术地说是在特征为0的域上)的代数簇时,双有理映射的灵活性允许你将奇异簇和没有任何奇点的光滑射影簇联系起来。用这种方式“消解”代数簇是非常有用的工具,从而考虑把互相能双有理联系起来的簇放在同一类是有道理的。
Birkar的研究领域是双有理几何,这是专门研究用这种方式分类代数簇的。特别地,数学家期望证明每一个射影代数簇都双有理地联系到某个特殊的好簇,这些好簇是由三种基本组件组成的。对于最简单的(一维复)簇,这已经被19世纪末的数学家黎曼6证实。二维的情形在20世纪初已经搞清楚。随着时间的推移,三维的情形在20世纪70年代到20世纪90年代之间才了解清楚。四维及以上的情形仍然有很多关键问题,而Birkar恰是在这一领域做出了重要贡献。这一领域的目标是证明所谓的极小模型纲领是可行的,这是一种专门设计的将任何代数簇转变为上述三种漂亮的基本组件的算法。
Birkar生于1978年,生长于伊朗的库尔德斯坦省,在伊朗和伊拉克战争混乱时期上学。 里约热内卢举办的国际数学家大会开幕式上,Birkar在获奖视频中说道:“对于一个想要发展数学兴趣的小孩来说,战火纷飞的库尔德斯坦省并不是一个好地方。”是他的哥哥教了他在学校里没有见过的更高级数学,后来他在德黑兰大学学习数学。2000年,他移居到了英国。在英国,他被赋予难民身份并完成了他的博士学位。如今他是剑桥大学纯数学与数理统计系7的教授。他因而成为了我们的邻居,因此我们对他取得的惊人成就感到非常自豪。祝贺 Caucher Birkar!
https://www.youtube.com/embed/j_edYZE43-I
https://www.dpmms.cam.ac.uk/~cb496/↩
https://plus.maths.org/content/maths-minute-complex-numbers↩
https://en.wikipedia.org/wiki/Algebraic_variety↩
http://en.wikipedia.org/wiki/File:Riemann_sphere1.jpg↩
https://en.wikipedia.org/wiki/Birational_geometry#Birational_maps↩
http://www-groups.dcs.st-and.ac.uk/history/Biographies/Riemann.html↩
https://www.dpmms.cam.ac.uk/↩
| 作者简介: | Marianne Freiberger,Editor of Plus. |
| 译者简介: | 张浩,博士毕业于中国科学院大学基础数学专业,现从事基础教育工作。 |
| 原文链接: | https://plus.maths.org/content/test-1-0 |




