林开亮

在前两期

中国剩余定理

求一术与方程术

我们分别介绍了初等数论中的两个基本结果，中国剩余定理与求一术（及其推广方程术）。与其说它们是定理，还不如说它们是算法。算法与普通的定理有个差别，算法应用起来是要操作整个过程，而定理可能只需要你会用最终结论。所以你要掌握算法，就免不了要走一遍程序。也正是这个原因，不会跳跃的计算机很容易理解算法。记得编程大师高德纳(D. E. Knuth)有句名言：

所谓科学，就是能够教会计算机的东西。

他还说（大意）：只有当一个教师能够教会计算机了，才能教明白学生。

高德纳

今天我们介绍初等数论中一个地地道道的定理，历史上著名的欧拉定理。大数学家欧拉(Euler)有许多定理，我们这里所指的是下一个：

欧拉定理：设$n$是正整数，$a$是一个整数，且$a$与$n$互素，则 $$a^{\varphi (n)}\equiv 1\pmod{n}$$ 其中$\varphi (n)$（$\varphi$是希腊字母，发音即 wifi 的fi )是欧拉函数，表示$1,2,\cdots,n$中与$n$互素的数的个数。

$$\equiv$$ 这里看起来像汉字“三”的记号是同余记号，由高斯（Gauss）在1801年首次引进。同余式（可读作：$a$与$b$模$m$同余，或$a$模$m$同余于$b$)。

$$a\equiv b\pmod{m}$$ 表示$a-b$是$m$的倍数，或者可以等价的说, $a$除以$m$的余数（用带余数的除法）与$b$除以$m$的余数相同。

其实在生活中，我们经常用到同余的观念。例如，你如果问一个小朋友：假设现在是中午12点，那么再过12个钟头，是几点？他很可能回答说，是0点（如果他有0的概念的话）。这是因为一天有24个小时，在模24的意义下，24与0是一样的。

一个更简单而往往被忽略的，是下述电影海报上的等式：在模2意义下，2=0. 它的一个生活常识解释是：开关的运算法则是，两次操作，回复原位。模2运算同时也是数理逻辑的基础（也许常常称为布尔运算）。

又如今年（2018年）国庆节是星期一，由此可知明年的国庆节是星期二，因为 $$365 \equiv 1 \pmod{7}$$

Question1: 2020年的国庆节星期几？（注意，这里有个坑）

再如，如果我告诉你某个人的出生年份，那么你可以推出他的属相。例如，

高斯出生于1777年，那么不难根据 $$1777 \equiv 2017 \pmod{12}$$

推出高斯属鸡（2017年是鸡年）。

Question2:出生于1642年的牛顿(Newton)的生肖是什么？

现在回到欧拉定理本身，我们需要理解的，是欧拉函数$\varphi (n)$，这个函数表示$1,2,\cdots,n$中与$n$互素的数目的个数。例如，若取$n=12$, 则不难发现，在$1$—$12$中，与$12$互素的数只有$1,5,7,11$一共$4$个，所以$\varphi (n)=4$。

如果知道了n的全部素因子（这里有一个相关的定理，算术基本定理），那么很容易求出。我们有下述结果：

定理：设$n$的全部不同素因子为$p _ { 1 } , \dots , p _ { k }$，则 $$\varphi ( n ) = n \left( 1 - \frac { 1 } { p _ { 1 } } \right) \cdots \left( 1 - \frac { 1 } { p _ { k } } \right)$$ 这个定理的一个特例是n=p是素数的情况，此时 $$\varphi ( p ) = p - 1$$

这一点根据定义也很容易看出。在这个特殊情况下，欧拉定理退化为费马小定理：

费马小定理（第一种表述） 设$p$是一个素数，若$a$与$p$互素，则 $$a ^ { p - 1 } \equiv 1 \pmod{p} $$ 一个等价的表述如下：
费马小定理（第二种表述） 设$p$是一个素数， 则对任意的自然数$n$有 $$n ^ { p } \equiv n \pmod{p} $$

注：历史上先有费马小定理，而后有欧拉定理，因此欧拉定理也被称为费马-欧拉定理。

Question3: 用数学归纳法证明第二种表述的费马小定理。

欧拉定理（或费马-欧拉定理）的证明，可以在维基百科查到，我们这里不再展开，见网页Euler Theorem。

要指出的是，高观点下的欧拉定理，是一个群论定理（拉格朗日定理）的特殊情形。这个定理说，一个有限阶群，每个元素的阶数都整除群的阶数。这里的群，是整数在模$n$下的（乘法）可逆元（也就是与$n$互素的同余类）构成的群，其阶数恰好是$\varphi (n)$。要说明这一点，相当于要证明下述结果：

定理：设$b$是正整数， 则同余方程$a x \equiv 1 \pmod b$，有整数解当且仅当$a,b$互素。

Question4: 请利用第2期介绍的求一术或方程术证明上述定理。

另一方面，我们也可以对模$n$下的（乘法）可逆元给出另一个解释。这就涉及到另一个群，即整数在模n下的加法群。这个群是一个循环群（注：循环群是最简单的一类群），其阶数恰好等于$n$。 这个循环群的生成元，恰好就是那些与n互素的同余类。以n=12为例，容易看出，$1,5,7,11$恰好是模$12$的加群的生成元。这一点（主要是$5$)很早就被中国古代的音律学家发现了，在《吕氏春秋》之《音律》篇中我们可以读到：

黄钟生林钟，林钟生太簇，太簇生南吕，南吕生姑洗，姑洗生应钟，应钟生蕤宾，蕤宾生大吕，大吕生夷则，夷则生夹钟，夹钟生无射，无射生仲吕。

指的就是，在模$12$的加群下, 从$7$出发，反复加$7$, 将遍历各个同余类，依次得到

7（黄钟）→14=2（林钟）→9（太簇）→16=4（南吕）→11（姑洗）→18=6（硬钟）→13=1（蕤宾）→8（大吕）→15=3（夷则）→10（夹钟）→17=5（无射）→12（仲吕）

如下图所示（引自程贞一《黄钟大吕》，王翼勋译，上海科技教育出版社，104页）：

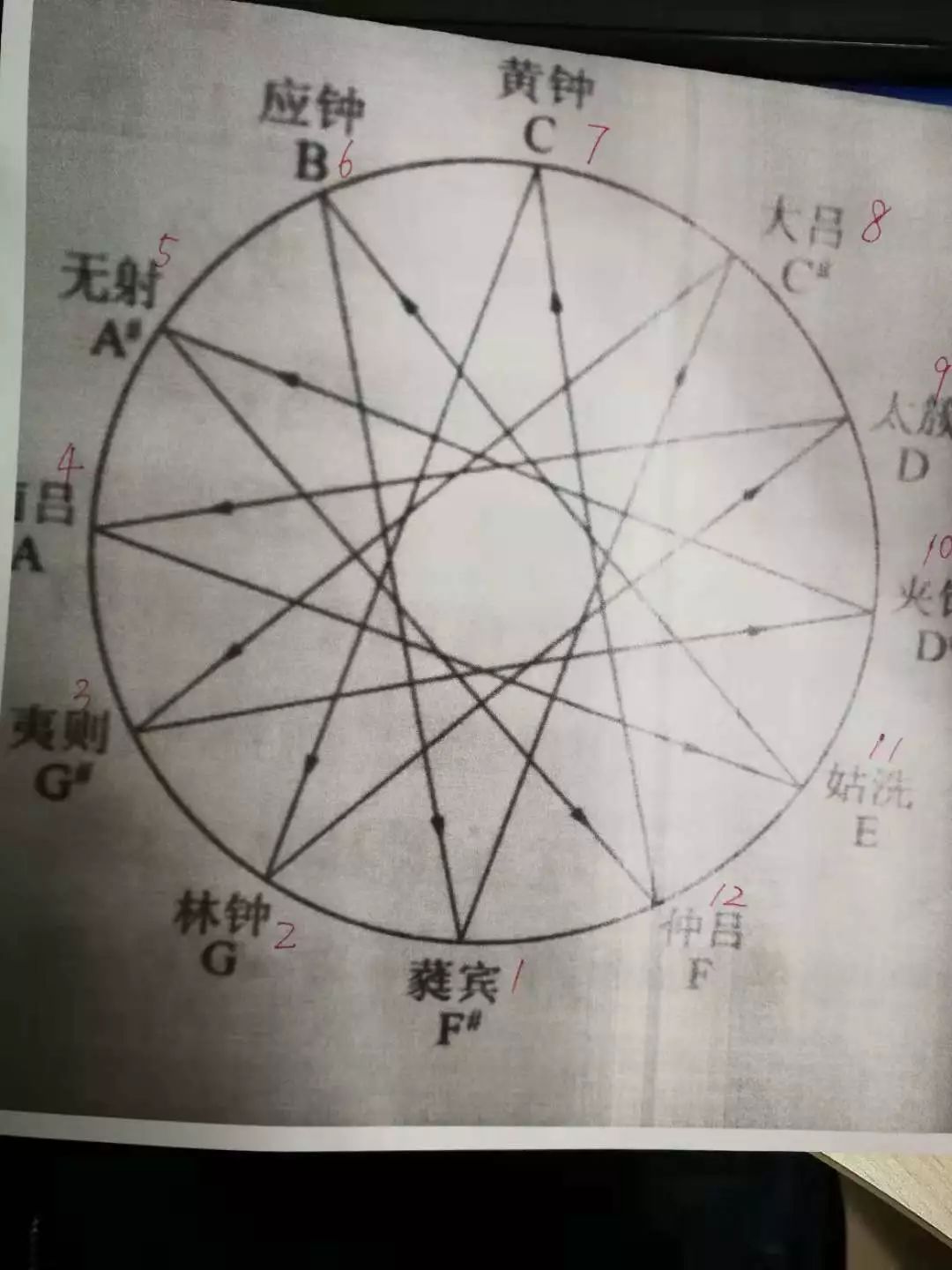
Question5: 写出在模$12$的加群下, 从$5$出发，反复加$5$, 依次得到的各个同余类。

注：应该指出，在音律中有对称，有群（你可以大致认为，群就是对称生成的）。这里的模$12$加群与十二平均律有关。在几何上对应着一个正十二边行的旋转群。正如正十二边形的对称，除了旋转，还有关于对称轴的反射；音律群里除了对应着旋转的变调，还有对应着反射的转位。因此，主导音乐的对称群是正十二边形的对称群，也就是24阶的二面体群。对此有兴趣的读者，我们推荐一篇漂亮的文章：

Alissa S. Crans、Thomas M Fiore、Ramon Satyendra的二面体群作

Alissa S. Crans、Thomas M. Fiore、Ramon Satyendra，音乐中的二面体群作用，中译文收入“数学与人文”丛书第17辑《数学的艺术》，丘成桐；刘克峰；杨乐；季理真 李方主编，高等教育出版社，2015年。

最后，回到欧拉定理本身，为加深你对这个定理的印象，我们再给出一个练习：

Question6: 已知 2017是素数，求 $$2019 ^ { 2018 } \equiv ? \pmod{2017}$$

小结：欧拉定理体现了这样的观念，在整数中存在着结构（在这里，就是群）。有了这样的观点，许多东西理解起来会比较简单而深刻，因为一些表面上不同的东西可以得到统一。陈省身先生曾经说，真正重要的观念是很少的，毫无疑问，群是其中一个。

P. S. 写到这里，我回想起从前念书时，我读到的第一个很喜欢的观念，就是群作用。当时我在田代军老师的指引下，自学Jacobson的《基础代数》中译本。